การวิเคราะห์สหสัมพันธ์
บ่อยครั้งที่ต้องหาความความสัมพันธ์ระหว่างตัวแปรตั้งแต่สองตัวแปรขึ้นไป การวิเคราะห์สหสัมพันธ์ซึ่งเป็นเครื่องมือพื้นฐานในการวัดว่าตัวแปรทั้งสองมีความแตกต่างกันอย่างไรในความสัมพันธ์ซึ่งกันและกัน
Scatter Plots
Scatter Plots หรือแผนภาพการกระจายเป็นเครื่องมือในการวิเคราะห์ความสัมพันธ์
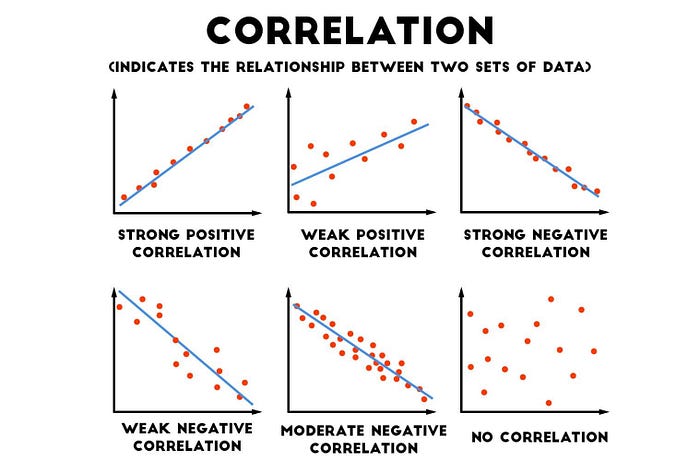
สังเกตได้ว่าภาพการกระจายจะแสดงเป็นจุดและจุดแต่ละจุดจะไม่เชื่อมต่อกัน ภาพการกระจาย จะแสดงเฉพาะการสังเกตจริงของชุดข้อมูลทั้งสองที่พล็อตเป็นคู่ เราสามารถแสดงความสัมพันธ์ของสองตัวแปรได้ด้วย ค่าสหสัมพันธ์
ค่าสหสัมพันธ์
การวิเคราะห์สหสัมพันธ์ คือการหาความสัมพันธ์ของตัวแปรซึ่งแสดงด้วยตัวเลข ค่าสัมประสิทธิ์สหสัมพันธ์คือการวัดว่าชุดข้อมูลสองชุดมีความสัมพันธ์กันมากเพียงใด และบ่งบอกถึงทิศทางระหว่างสองตัวแปร ค่าสัมประสิทธิ์สหสัมพันธ์สามารถมีค่าสูงสุด 1 และค่าต่ำสุดคือ −1 ค่าสัมประสิทธิ์สหสัมพันธ์ที่มากกว่า 0 หมายถึงการเชื่อมโยงเชิงเส้นเชิงบวกระหว่างสองตัวแปร: เมื่อตัวแปรหนึ่งเพิ่มขึ้น (หรือลดลง) อีกตัวแปรก็มีแนวโน้มที่จะเพิ่มขึ้น (หรือลดลง) ค่าสัมประสิทธิ์สหสัมพันธ์ที่น้อยกว่า 0 หมายถึงการเชื่อมโยงเชิงเส้นเชิงลบระหว่างสองตัวแปร: เมื่อตัวแปรหนึ่งเพิ่มขึ้น (หรือลดลง) อีกอันมีแนวโน้มที่จะลดลง (หรือเพิ่มขึ้น) ค่าสัมประสิทธิ์สหสัมพันธ์เป็น 0 บ่งชี้ว่าไม่มีความสัมพันธ์เชิงเส้นระหว่างสองตัวแปร 2
ในการศึกษาความสัมพันธ์จาข้อมูลในอดีตหรือข้อมูลตัวอย่าง เราจำเป็นต้องใช้ความแปรปรวนร่วมของข้อมูล ความแปรปรวนร่วม ของ X และ Y สำหรับตัวอย่างที่มีขนาดเท่ากับ n สามารถหาได้จากสมาการด้านล่าง
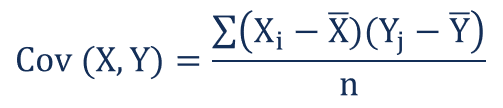
ความแปรปรวนร่วมของตัวอย่างคือค่าเฉลี่ยของผลคูณของความเบี่ยงเบน-v’ตัวแปรสุ่มสองตัว เราสามารถหาค่าสมประสิทธิความแปรปรวนด้วยสมการต่อไปนี้
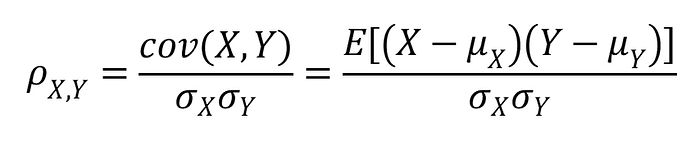
ค่าสัมประสิทธิ์สหสัมพันธ์คือความแปรปรวนร่วมของสองตัวแปร (X และ Y) หารด้วยผลคูณของค่าเบี่ยงเบนมาตรฐานตัวอย่าง เช่นเดียวกับความแปรปรวนร่วมสัมประสิทธิ์สหสัมพันธ์เป็นตัวชี้วัดของการสัมพันธ์เชิงเส้น อย่างไรก็ตามค่าสัมประสิทธิ์สหสัมพันธ์มีข้อดีคือเป็นตัวเลขธรรมดาโดยไม่มีหน่วยวัด ที่ไม่มีหน่วยเนื่องจากเป็นผลมาจากการหารความแปรปรวนร่วมด้วยผลคูณของส่วนเบี่ยงเบนมาตรฐาน
ข้อจำกัดของ การวิเคราะห์สหสัมพันธ์
การวิเคราะห์สหสัมพันธ์วัดความสัมพันธ์เชิงเส้นระหว่างสองตัวแปร แต่อาจมีข้อจำกัดข้างอย่าง ตัวแปรสองตัวสามารถมีความสัมพันธ์แบบไม่เชิงเส้นที่แข็งแกร่งและยังมีความสัมพันธ์ที่ต่ำมาก ตัวอย่างเช่นความสัมพันธ์ B = (A — 4) 2 เป็นความสัมพันธ์แบบไม่เชิงเส้นที่เปรียบเทียบกับความสัมพันธ์เชิงเส้น B = 2A — 4 ความสัมพันธ์แบบไม่เชิงเส้นระหว่างตัวแปร A และ B แสดงในรูปที่ 5 ต่ำกว่าระดับ 4 สำหรับ A ตัวแปร B จะลดลงตามค่าที่เพิ่มขึ้นของ A อย่างไรก็ตามเมื่อ A เป็น 4 ขึ้นไป B จะเพิ่มขึ้นเมื่อใดก็ตามที่ A เพิ่มขึ้น แม้ว่าตัวแปรทั้งสองนี้จะมีความสัมพันธ์กันอย่างสมบูรณ์ แต่ความสัมพันธ์ระหว่างตัวแปรก็คือ 0.5

หรือในบ้างครั้งหากมีข้อมูลผิดปกติ(outlier) จำทำให้ค่าที่ได้จากการวิเคราห์สหสัมพันธ์มีค่าที่ผิดปกติ

จากรูปด้านบน ข้อมูลส่วนใหญ่อยู่รวมกันเป็นกลุ่ม เราจะสังเกตได้ว่าข้อมูลแทบไม่มีความสัมพันธ์กัน หากเราสังเกตข้อมูลที่อยู่ในวงกลม ถ้าเราคำนวณค่าสัมประสิทธิ์สหสัมพันธ์สำหรับตัวอย่างข้อมูลทั้งหมดความสัมพันธ์นั้นจะเท่ากับ −0.0350 อย่างไรก็ตามหากเรากำจัดค่าผิดปกติทั้งสองออกไปความสัมพันธ์จะเท่ากับ −0.1489
ดังนั้นค่าสัมประสิทธ์สหสัมพันธ์ค่อนข้างอ่อนไหวต่อค่าผิดปกติ ในการวิเคราะห์ความสัมพันธ์เราอาจจะรายงานทั้งค่าสหสัมพันธ์ทั้งแบบตัดค่าปกติและไม่ตัดค่าปกติ โดยค่าผิดปกติอาจให้ข้อมูลเกี่ยวกับความสัมพันธ์ในช่วงที่สถานการณ์ไม่ปกติอาทิในกรณีอาจเป็นตอนที่ตลาดมีปัญหา ดังนั้นในกรณีนี้จึงเป็นการสมเหตุสมผลที่จะรายงานค่าของความสัมพันธ์ซึ่งรวมและไม่รวมค่าผิดปกติ
การทดสอบนัยสำคัญของค่าสัมประสิทธิ์สหสัมพันธ์
เราสามารถทดสอบระดับนัยสำคัญของค่าสัมประสิทธิ์สหสัมพันธ์ด้วยตัว สถิติทดสอบ t ด้วยสมการด้านล่างนี้ โดยมีองศาความเป็นอิสระเท่ากับ n -2


